Kode Program C++: Mengurutkan Angka (Algoritma Merge Sort)

Algoritma Merge Sort: Mengurutkan Angka dengan Efisiensi O(n log n) dalam C++

Pendahuluan

Dalam pemrograman dan ilmu komputer, mengurutkan data merupakan salah satu operasi dasar yang sering dilakukan. Pengurutan data dapat dilakukan dengan berbagai algoritma, salah satunya adalah algoritma merge sort. Algoritma merge sort terkenal dengan efisiensi dan kestabilannya dalam mengurutkan data dalam jumlah besar. Artikel ini akan membahas implementasi algoritma merge sort dalam bahasa pemrograman C++ secara detail.

Memahami Algoritma Merge Sort

Algoritma merge sort bekerja dengan prinsip memecah masalah pengurutan menjadi sub-masalah yang lebih kecil, kemudian menggabungkan hasil pengurutan sub-masalah tersebut hingga seluruh data terurut. Proses ini dapat digambarkan sebagai berikut:

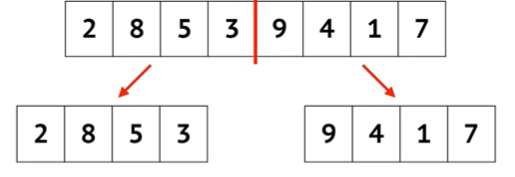
1. Pembagian (Divide): Data dibagi menjadi dua bagian yang sama besar.
2. Penaklukan (Conquer): Kedua bagian data tersebut diurutkan secara rekursif menggunakan algoritma merge sort.
3. Penggabungan (Merge): Setelah kedua bagian data terurut, kedua bagian tersebut digabungkan menjadi satu data yang terurut.

Proses pembagian, penaklukan, dan penggabungan ini dilakukan secara berulang hingga seluruh data terurut.

Implementasi Algoritma Merge Sort dalam C++

Berikut ini adalah implementasi algoritma merge sort dalam bahasa pemrograman C++:

#include <iostream>
#include <vector>

using namespace std;

// Fungsi untuk menggabungkan dua array yang terurut
void merge(vector<int>& arr, int low, int mid, int high) {
  // Tentukan ukuran kedua array yang akan digabungkan
  int n1 = mid - low + 1;
  int n2 = high - mid;

  // Buat array sementara untuk menyimpan data dari kedua array
  vector<int> left(n1);
  vector<int> right(n2);

  // Salin data dari array asli ke array sementara
  for (int i = 0; i < n1; i++) {
    left[i] = arr[low + i];
  }
  for (int i = 0; i < n2; i++) {
    right[i] = arr[mid + 1 + i];
  }

  // Gabungkan dua array sementara kembali ke array asli
  int i = 0, j = 0, k = low;
  while (i < n1 && j < n2) {
    if (left[i] <= right[j]) {
      arr[k] = left[i];
      i++;
    } else {
      arr[k] = right[j];
      j++;
    }
    k++;
  }

  // Salin elemen yang tersisa dari kedua array sementara ke array asli
  while (i < n1) {
    arr[k] = left[i];
    i++;
    k++;
  }
  while (j < n2) {
    arr[k] = right[j];
    j++;
    k++;
  }
}

// Fungsi untuk mengurutkan array menggunakan algoritma merge sort
void mergeSort(vector<int>& arr, int low, int high) {
  if (low < high) {
    // Hitung titik tengah array
    int mid = (low + high) / 2;

    // Panggil fungsi merge sort secara rekursif untuk kedua bagian array
    mergeSort(arr, low, mid);
    mergeSort(arr, mid + 1, high);

    // Gabungkan kedua bagian array yang telah diurutkan
    merge(arr, low, mid, high);
  }
}

int main() {
  // Buat array yang ingin diurutkan
  vector<int> arr = {10, 7, 8, 9, 1, 5};

  // Tampilkan array sebelum diurutkan
  cout << "Array sebelum diurutkan: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }
  cout << endl;

  // Panggil fungsi merge sort untuk mengurutkan array
  mergeSort(arr, 0, arr.size() - 1);

  // Tampilkan array setelah diurutkan
  cout << "Array setelah diurutkan: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }
  cout << endl;

  return 0;
}

Analisis Kompleksitas Algoritma Merge Sort

Algoritma merge sort memiliki kompleksitas waktu O(n log n), di mana n adalah jumlah elemen dalam array. Hal ini berarti bahwa waktu yang dibutuhkan untuk mengurutkan array menggunakan merge sort akan berbanding lurus dengan logaritma jumlah elemen dalam array. Ini adalah salah satu algoritma pengurutan yang paling efisien dan stabil.

Kesimpulan

Algoritma merge sort merupakan algoritma pengurutan yang efisien dan stabil yang dapat digunakan untuk mengurutkan data dalam jumlah besar dengan kompleksitas waktu O(n log n). Implementasi algoritma merge sort dalam bahasa pemrograman C++ yang telah dijelaskan dalam artikel ini dapat digunakan untuk berbagai keperluan, termasuk pemrograman kompetitif, pengolahan data, dan analisis data.